図形の作成
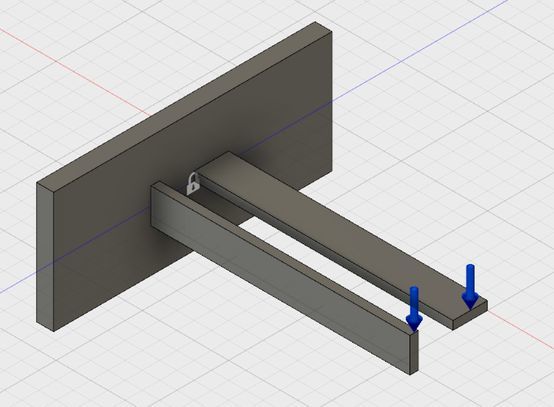
まずは断面が5mm×20mmで長さが150mmの図面を作成し、端部に集中荷重が加わるようにします。このとき集中荷重が加わる方向は比較のため、短辺のものと長辺のものを用意します。
シミュレーションの設定
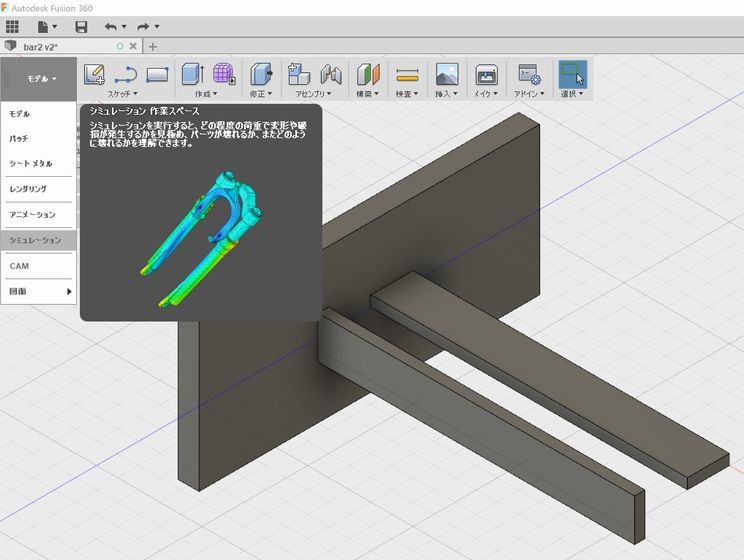
左上に「デザイン」とある灰色の四角形をクリックして「シミュレーション」を選択します。
静的応力
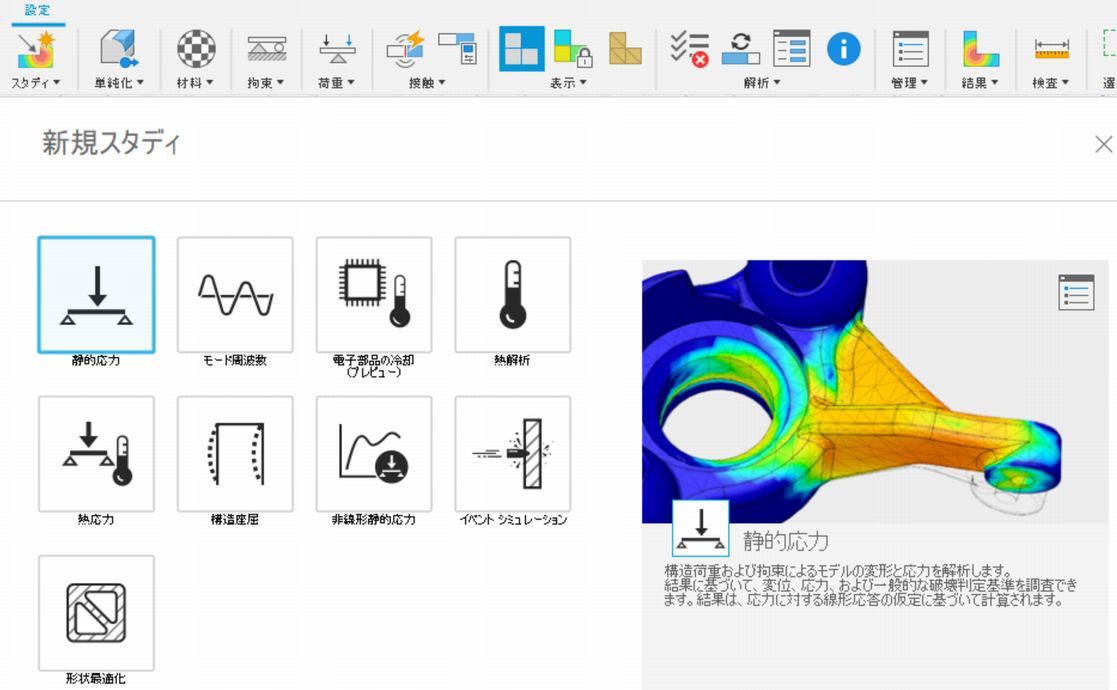
左上にある「静的応力」を選びます。ここでは材料の荷重を加えたときの「変形」と「応力」を解析します。
静的応力の選定
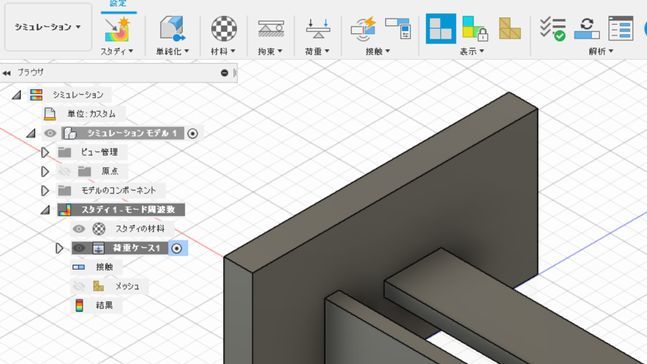
上部に新たなコマンドが現れますので、「マテリアル(=材料)」「拘束」「荷重」などを設定していきます。
マテリアルの選定
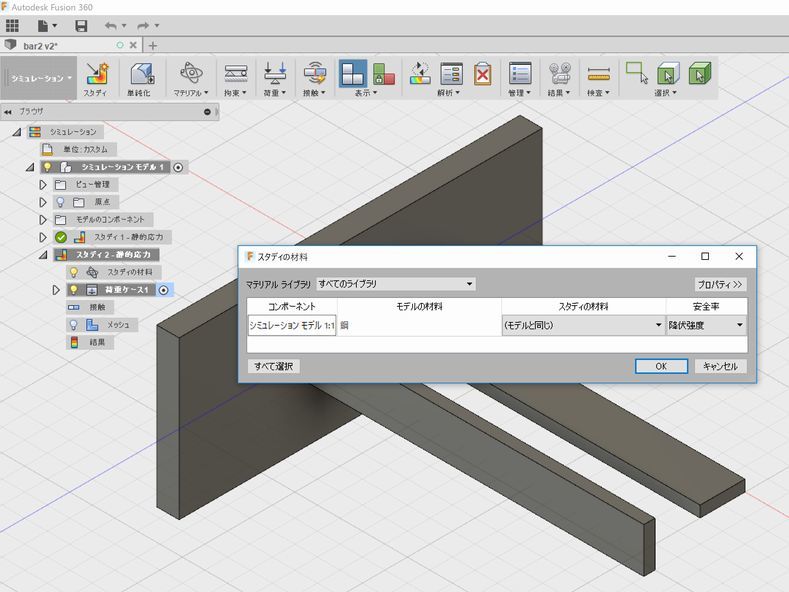
マテリアルをクリックして材料を選定します。ここでは鋼を選定しました。
スタディの材料
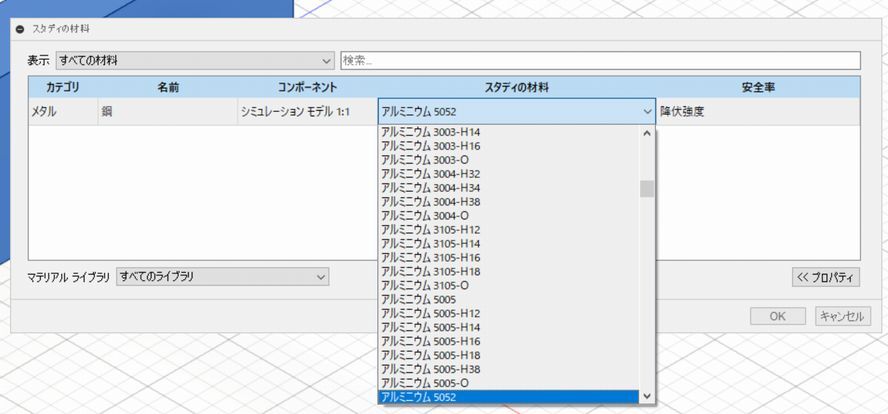
スタディの材料の箇所をクリックすると材料の一覧が出てくるので、初期設定の鋼以外のものを選択するときにはこちらから選びます。ただし、JISの型番が詳しく出てくるので、材料に関する知識が必要になります。
拘束条件の設定
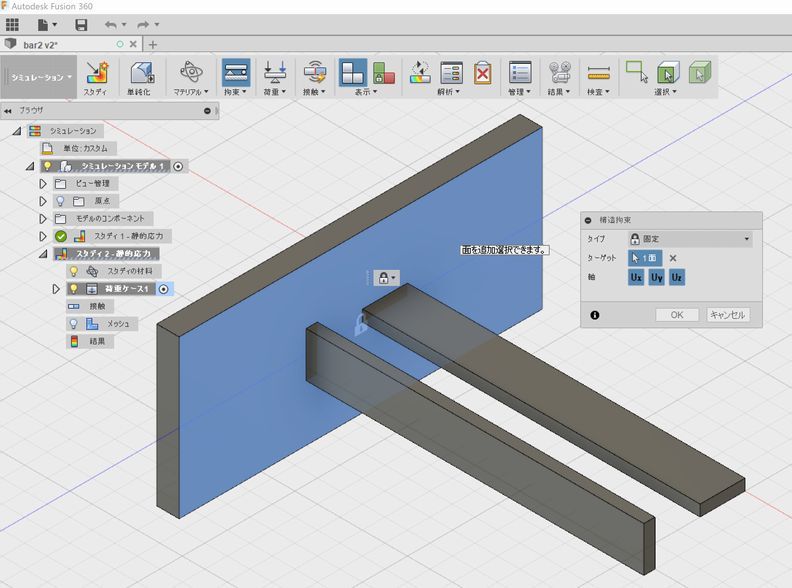
2つのはりの端部に共通な面を固定するため、拘束条件をクリックして、一面を固定します。
2つのはりの端部に集中荷重を加える
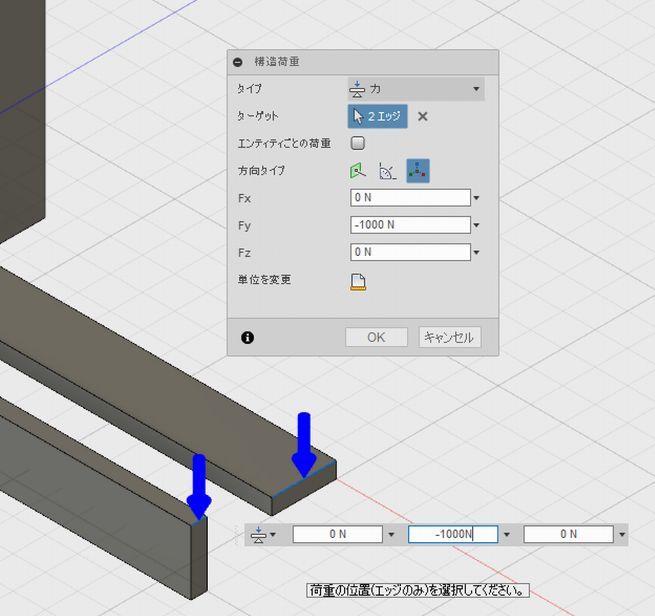
「荷重」をクリックしてから「構造荷重」をクリックします。2つのはりの端部(エッジ)をして、下向き(Y方向)に荷重を加えます。このとき下向きなので-をつけます。ここでは1000Nを加えてみます。
解析の事前チェック
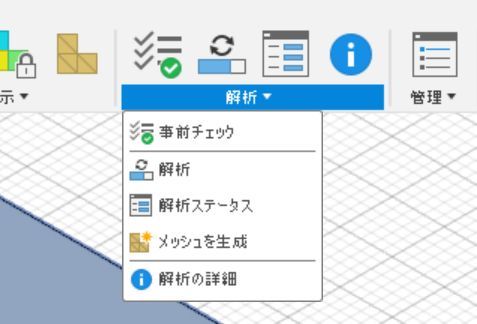
解析を始める前に、「解析」をクリックしてから「事前チェック」を選定します。不足している条件がないかをここでチェックします。
事前チェックがOKの確認
このような画面が出たら事前チェックがOKです。
解析の開始
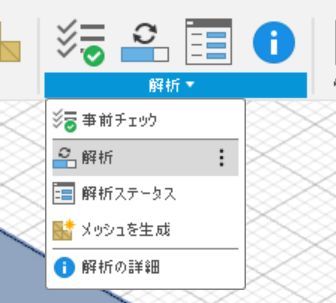
「事前チェック」の下にある「解析」をクリックして解析を開始します。モデルの大きさに応じて、いくらかの時間がかかります。
解析の開始2
最終的な開始の確認画面です。これでよろしければ、「1スタディを解析」をクリックすると解析が開始されます。
解析結果~安全率の表示
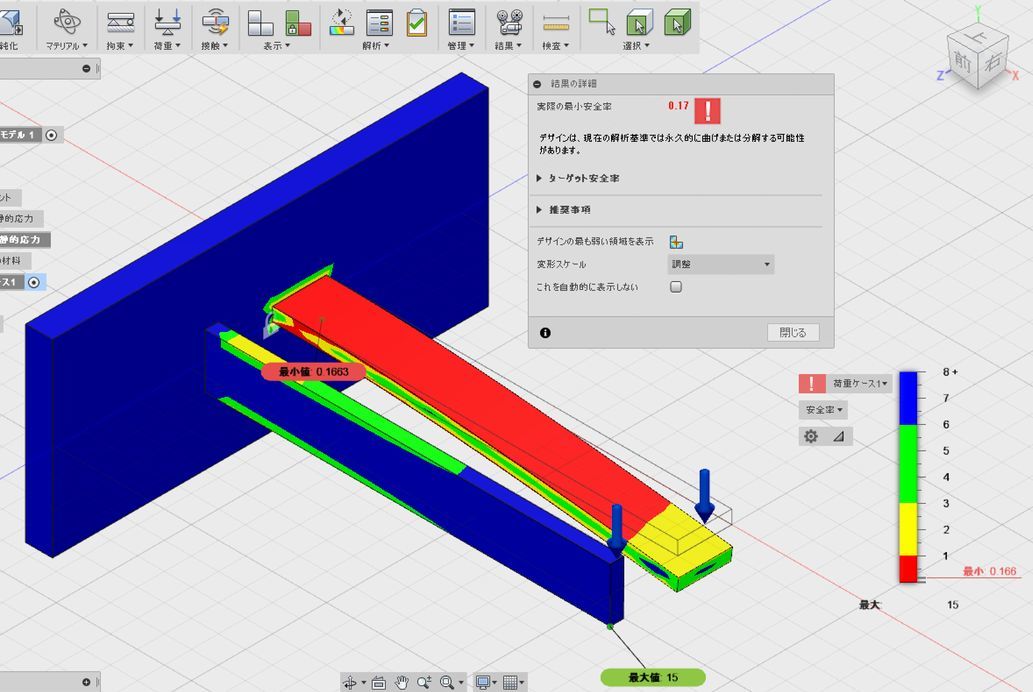
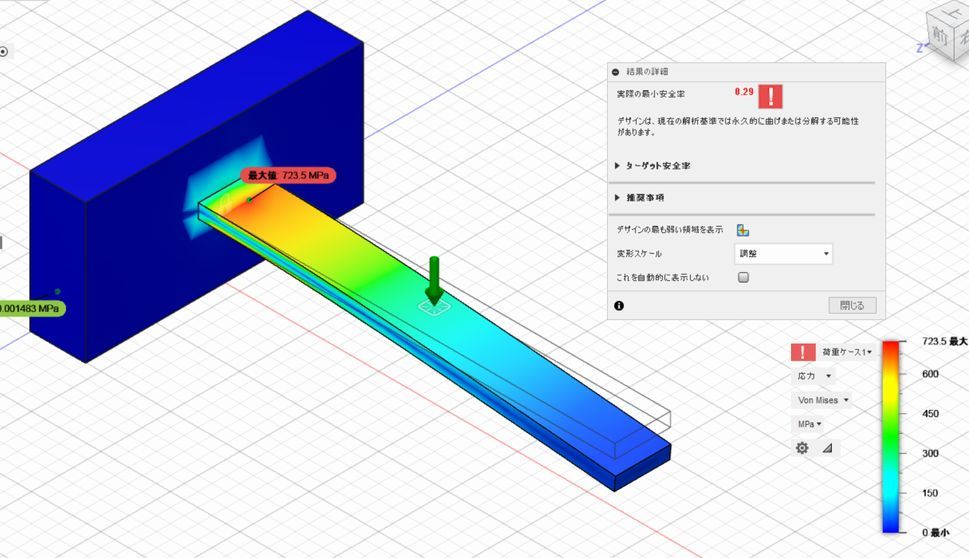
この解析には1分ほどかかりました。解析結果はいくつかの表示形式があります。最初に出てくるのは「安全率」です。ここでは赤い部分がかなり危険だという指摘がされました。
応力の表示
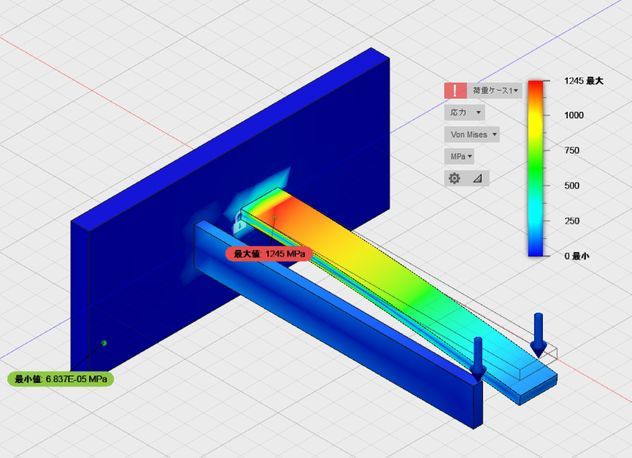
「安全率」の表示をクリックすると「応力」の分布図を表示できます。こちらが応力(=単位面積あたりにはたらく力)の分布図になります。長辺に集中荷重を加えているはりの根元付近に大きな応力がはたらいていることがわかります。
変位の表示
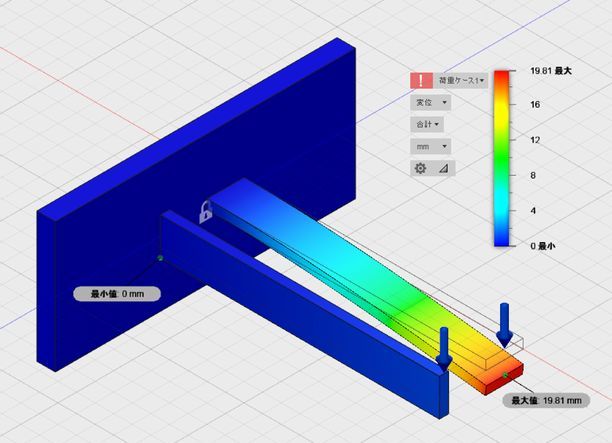
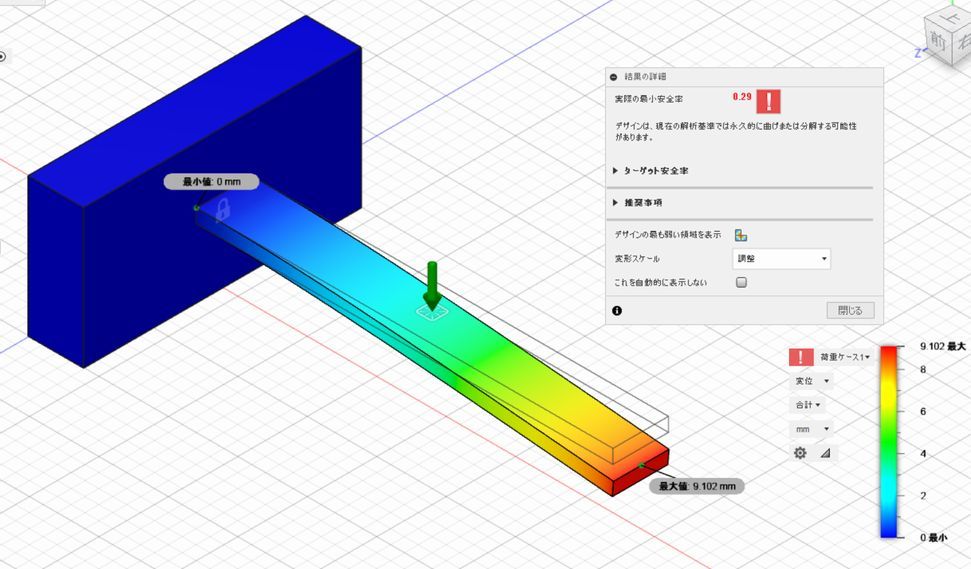
「安全率」「応力」の次は、「変位」の表示です。長辺に集中荷重を加えたはりの端部が大きく変形していることがわかります。
ひずみの表示
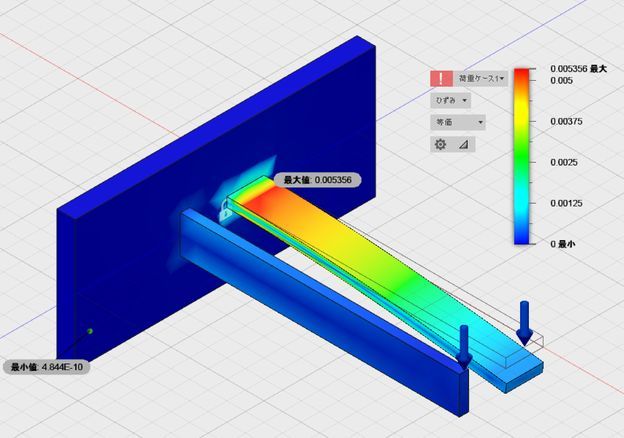
こちらがひずみ(元の長さからの長さ変化分)になります。
断面係数について
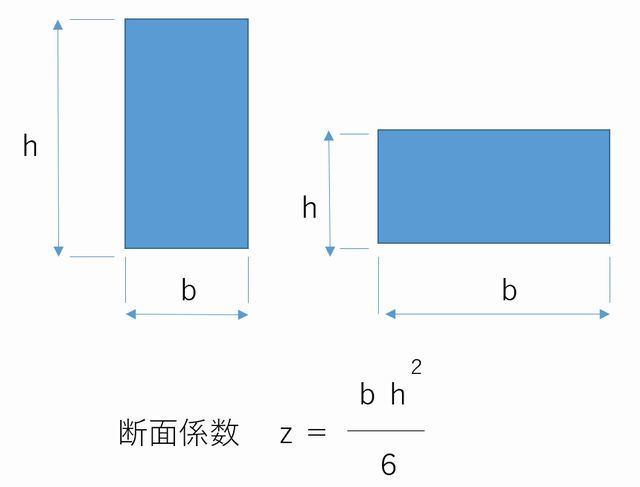
このシミュレーションからは、同じ断面形状であっても、曲げる方向によって曲がりやすさが異なることがわかります。すなわち、同じ長方形の断面形状でも、長辺よりも短辺に荷重が加わるように活用したほうが、曲げに強いことがわかります。この断面のことを断面係数といい、各断面形状に応じて公式が定められています。長方形断面の断面係数zを求める公式は図のようになります。ここで断面係数の値が大きいほど曲げに強いということになります。すなわち、縦方向のhを2乗するのでこの図で荷重が上方向から加わる場合、縦長に活用した方が曲げに強くなるのです。確認のため実際の数値を入れて計算してみましょう。
断面係数の計算
縦長で使用する場合、z1=(5×20×20)/6=333.3 ㎜3 (3は右上の3乗)
横長で使用する場合、z2=(20×5×5)/6=83.3 ㎜3 (3は右上の3乗)
よって、縦長で使用する場合の方が、断面係数が大きく、曲げに強いことがわかります。
横長で使用する場合、z2=(20×5×5)/6=83.3 ㎜3 (3は右上の3乗)
よって、縦長で使用する場合の方が、断面係数が大きく、曲げに強いことがわかります。
応力の求め方
なお、シミュレーション結果で「応力」とある図は、
応力σ=曲げモーメントM/断面係数zで求めた結果です。
ここで曲げモーメントMとは、荷重F×荷重が加わる長さLのことです。
応力σ=曲げモーメントM/断面係数zで求めた結果です。
ここで曲げモーメントMとは、荷重F×荷重が加わる長さLのことです。
等分布荷重の場合
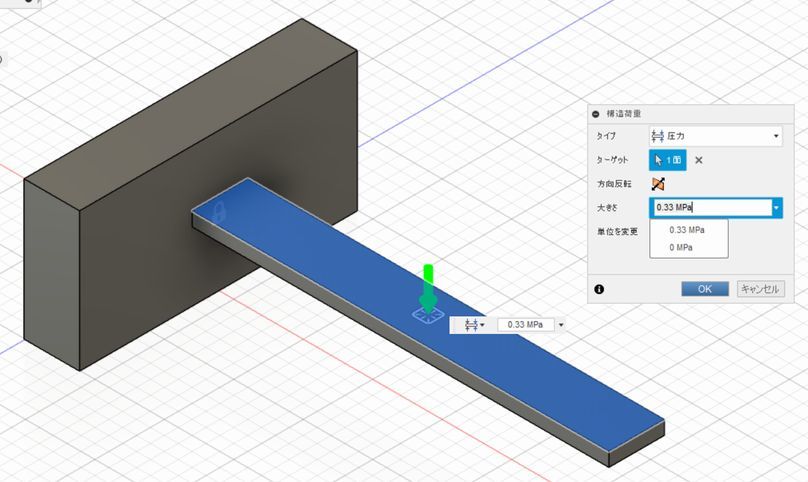
ある面積に等しい大きさの荷重が加わる等分布荷重をうけるはりの応力解析を行う場合には、「構造荷重」のタイプを「力」から「圧力」に変更して、その大きさをMPaの単位で入力します。ここでのはりの面積は20×150=3000mm2、集中荷重では1000Nであったため、それに合わせると、1000/3000
=0.33N/mm2となるので、ここではこの値を使用します。
解析結果(安全率)
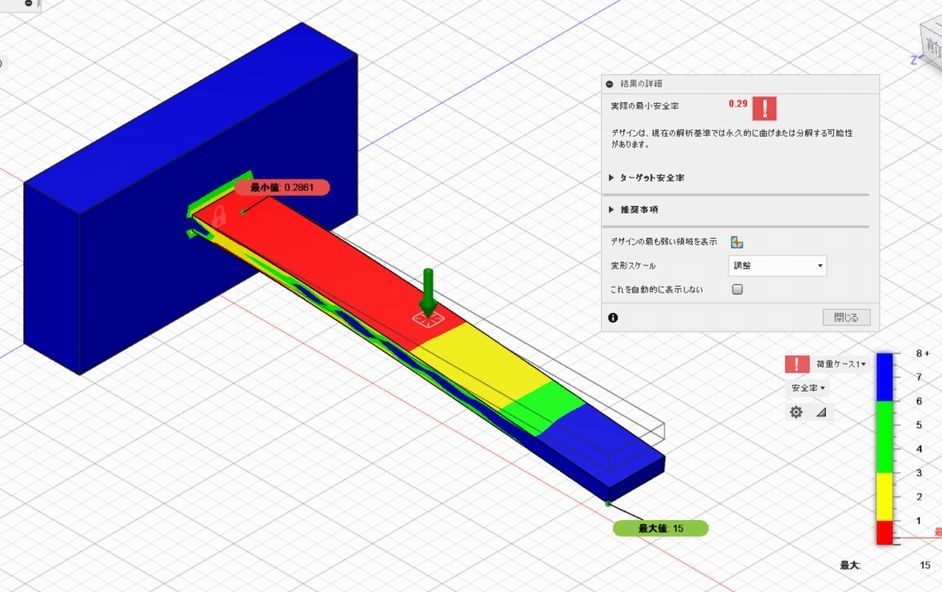
解析結果(変位)
解析結果(応力)